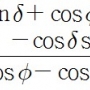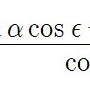(1) 지구 중심 좌표와 관측자 중심 좌표
지구 중심 좌표는 지구 중심에서 천체를 보았을 때의 좌표입니다. 이 좌표의 중심은 지구의 한 가운데에 있습니다. 천체의
위치를 계산할 때 주로 쓰이며 (책으로 인쇄된) 대부분의 천체력은 지구 중심 좌표로 천체(행성, 달, 위성)의 위치를 표기하고
있습니다.
관측자 중심 좌표는 관측지가 중심이 되는 좌표입니다. 관측지는 지구의 표면이나 공중에 있으므로 관측자 중심 좌표로 표시한
천체의 좌표는 지구 중심 좌표로 나타낸 좌표와 다릅니다. 이 차이는 시차(視差)에 의해 생기는 것으로, 특히 가까이에 있는
천체에서 두드러집니다. 지구와 가까운 달의 경우에 이 차이는 최대 1°에 이르며 해는 약 8"의 시차가 생깁니다.
(2) 관측지의 측지 위도와 지심 위도
관측지의 위치는 위도와 경도로 간단히 나타낼 수 있습니다. 경도는 본초자오선과 관측지 사이가 동서로 얼마나 떨어져 있는지를 나타내는 각도이고 위도는 적도와 남북으로 얼마나 떨어져 있는지를 나타내는 각도입니다.
이 가운데 위도는 측정하는 기준에 따라 측지 위도(Geodetic latitude)와 지심 위도(Geocentric latitude)로 나눌 수 있습니다(정확히는 측지 위도, 지리 위도, 지심 위도, 천문 위도로 나뉩니다. 천문위도는 지오이드에 수직인 직선이 적도면과 이루는 각도이고 지리위도는 지평면에 수직인 선이 적도면과 이루는 각도입니다. 지리 위도는 측지 위도와 거의 같고 천문 위도는 이름과는 달리 천문 계산에는 잘 쓰이지 않습니다).
측지 위도는 지구를 타원체라고 가정하고 타원체의 표면이 이루는 평면에 수직인 직선과 지구의 적도면이 만나는 각도로 정의합니다. 측지 위도는 지도의 제작에 쓰이고 있습니다. 지심 위도는 지구의 중심에서 측정한 위도입니다. 지구는 완전한 공 모양이 아니므로 지심 위도는 측지 위도와는 약간 다른 값을 가지는데, 11.7' 까지도 차이가 날 수 있습니다.
▲ 지심 위도(φ')는 지리 위도(φ)
관측지의 위치 계산에는 편의상 지심 위도를 씁니다. 지심 위도(φ')는 측지 위도(φ)를 써서 계산할 수 있습니다(관측지의 해발고도가 0m인 경우).
tan φ' = (b2/a2) tan φ
이 식에서 a는 지구의 적도 반지름, b는 극 반지름입니다. 극 반지름 b는 지구의 편평도(f)를 알고 있으면 아래 식으로 계산할 수 있습니다.
b = a(1 - f)
여기에서 지구의 적도 반지름 a는 6378137m, 편평도 f는 1/298.257223563입니다(WGS84).
a = 6378137 (m)
f = 1 / 298.257223563
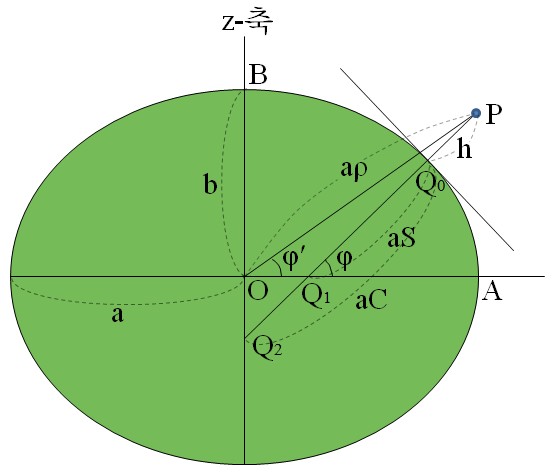
관측지의 고도(해발고도)가 0m가 아닌 곳에서는 지심위도와 지심거리(aρ)를 아래 식으로 계산할 수 있습니다(관측지의 해발고도를 h 라 가정).
먼저 계산에 쓰이는 변수 C와 S를 계산합니다.
자전축과 관측지 P의 거리 Px와 적도면과 관측지 사이의 거리 Pz는 아래 식으로 계산할 수 있습니다.
Px = (aC + h) cos φ
Pz = (aS + h) sin φ
직각삼각형 정리(피타고라스의 정리)와 삼각법에 의해 관측지의 지심거리 aρ와 지심 위도(φ')는 간단히 계산할 수 있습니다.
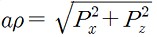
φ' = cos-1 (Px / aρ) = sin-1 (Pz / aρ)
정밀한 계산이 필요하다면 측지 위도(φ)는 지구의 극운동을 고려한 값을 써야합니다. 측지 위도는 아래 식으로 보정할 수 있습니다. 이 식은 근사식으로 고위도 지역에서는 쓸 수 없습니다.
φ = φITRS + (x cos λITRS - y sin λITRS)
λITRS와 φITRS는 세계측지계(또는 WGS84)로 나타낸 경도와 위도이고 x와 y는 각도로 나타낸 지구의 극운동 량입니다. 지구의 극운동량 값은 IERS에서 얻을 수 있습니다.
지구의 극운동 측정치 및 단기 예측값 얻기
IERS Bulletin A http://maia.usno.navy.mil/ser7/ser7.dat
IERS Bulletin B http://maia.usno.navy.mil/ser7/bulb.dat
경도 방향의 극운동은 이미 지방진항성시(LAST)를 계산할 때 반영하였으므로 따로 계산하지 않아도 됩니다.
(3) 관측지의 직교좌표 계산하기
적도좌표계로 나타낸 관측지의 직교좌표(xO, yO, zO)는 아래 식으로 계산할수 있습니다.
xO = aρ cos φ' cos θLST = (aC + h) cos φ cos θLST
yO = aρ cos φ' sin θLST = (aC + h) cos φ sin θLST
zO = aρ sin φ' = (aS + h) sin φ
이 식에서 θLST는 지방진항성시(LAST)입니다.
(4) 관측자 중심 좌표 구하기
천체의 지구 중심 적도좌표를 α(적경), δ(적위), rg(지심 거리)라 두면 지구 중심 적도 직교좌표(xg, yg, zg)는 아래 식으로 구할 수 있습니다.
xg = rg cos δ cos α
yg = rg cos δ sin α
zg = rg sin δ
천체의 관측자 중심 직교좌표(x', y', z')는 천체의 지구 중심 위치에서 관측지의 위치를 빼 주면 됩니다.
x' = xg - xO
y' = yg - yO
z' = zg - zO
이를 구면좌표로 바꾸어주면 천체의 관측자 중심 좌표를 얻을 수 있습니다. 구면 좌표로 바꾸는 방법은 아래와 같습니다. 관측자 중심 좌표로 나타낸 적경은 α', 적위는 δ', 천체와의 거리는 r' 입니다. 적경을 구할 때에는 역탄젠트 함수를 쓰는데, 잘못된 각도를 얻지 않도록 주의해야 합니다(사분면 문제).
α' = tan-1 (y' / x')
δ' = sin-1 (z' / r')
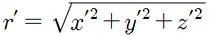
<참고자료>
1. The Astronomical Almanac for the year 2010 (Washington, D.C.; 2008)
2. J. Meeus, Astronomical Algorithms (Willmann-Bell, 1998)
3. 물리탐사 용어 사전 http://gpl.snu.ac.kr/mediawiki/index.php/%EC%B8%A1%EC%A7%80_%EC%9C%84%EB%8F%84_%28geodetic_latitude%29
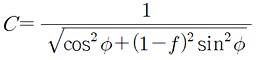
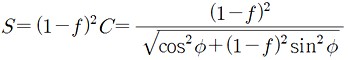

 적도좌표↔지평좌표
적도좌표↔지평좌표
 태양이 특정 황경을 통과하는 시점 계산
태양이 특정 황경을 통과하는 시점 계산