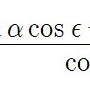천문학 - 항성시 계산(IAU1982)

IAU1982에서 결정된 항성시 계산법은 IAU2000/2006에서 결정한 방법보다는 조금 더 간단합니다. 오래된 방법이지만 아마추어용 성도 투영 프로그램에서는 여전히 널리 쓰이고 있습니다.

(1) 그리니치 평균항성시 계산(GMST)

그리니치 평균 항성시는 다음 식을 써서 계산합니다. T는 율리우스 세기로 나타낸 2000.0년으로부터의 시간 간격입니다.

T = (JD_TT - 2451545.0) / 36525

Θ₀는 UT로 0시의 그리니치 평균항성시, θ₀는 계산하고자 하는 시점의 그리니치 평균 항성시입니다. 아래 두 식은 표현 방법은 다르지만 근본적으로 동일한 식입니다. 실제로 쓰기에는 두번째 식이 조금 더 편리합니다. 항성시의 계산 단위는 도(degree)입니다. JD_UT는 율리우스 적일로 나타낸 날짜인데, UT로 나타낸 시간입니다.

Θ₀ = 100.46061837 + 36000.770053608T + 0.000387933T² - T³/38710000
θ₀ = 280.46061837 + 360.98564736629(JD_UT - 2451545.0) + 0.000387933T² - T³/3871000

Θ₀를 이용해서 계산한다면 계산 시점의 그리니치 항성시(θ₀)는 아래 식으로 계산할 수 있습니다.

θ₀ = Θ₀+ r' × H_(UT-0h)

H_(UT-0h)는 UT 0시로부터 경과한 시간입니다. 예를들어 UT로 14시라면 H_(UT-0h)의 값은 14시간이 됩니다. 계산에 쓸 때에는 단위를 잘 맞춰 주어야 합니다. 예를 들어 계산 단위로 도(degree)를 사용한다면 14에 15(= 360/24)를 곱해주어야 합니다.

r'는 항성시과 태양시의 길이 비율입니다. 보통 이 값으로 1.00273790935를 쓰면 됩니다. 이 비율은 아주 느리게 변화하는데, 아주 정밀한 계산이 필요하다면 이 변화를 반영할 수 있습니다. r'는 아래 식으로 구할 수 있습니다.

r' = 1.002737909350795 + 5.9006 × 10^-16T - 5.9 × 10^-15T²

(2) 그리니치 겉보기 항성시 계산(GAST, GST)

그리니치 겉보기 항성시는 그리니치 평균 항성시에 장동을 반영해주면 됩니다. GMST와의 차이가 각도로 10초 미만이므로 높은 정밀도가 필요하지 않다면 GMST를 그대로 써도 됩니다.

그리니치 겉보기 항성시는 아래 식으로 계산할수 있습니다.

θ = θ₀ + Δψ cos ε

이 식에서 Δψ는 장동으로 인한 황경의 변화량, ε는 계산 시점의 진황도경사각입니다. 이 식에서 장동 계산은 IAU1980에서 결정된 계산법을 써야하고, 진황도경사각 ε는 평균황도경사각(IAU1980)에 장동으로 인한 변화량을 보정한 값을 쓰면 됩니다. 아래 식으로 계산할 수 있습니다.