항성시는 우주에 고정된 기준을 두고 이 기준점에 대한 겉보기 운동으로 측정하는 시간 체계입니다.
항성시로 나타낸 하루(항성일)는 지구 공전의 영향으로 인해 태양시로 나타낸 하루(태양일)보다는 약간 짧습니다. 2010년을 기준으로 태양일과 항성일의 길이는 아래와 같습니다.
1 평균 태양일(24시간) = 1.00273790935 평균 항성일(24시간 3분 56.55537초)
항성시는 대강 4종류 정도로 나눌 수 있습니다.
그리니치 평균 항성시(GMST, Greenwich Mean Sidereal Time)
특정 시점에 경도 0도(본초자오선)에서 측정한 평균 항성시
그리니치 겉보기 항성시(GAST, GST, Greenwich Apparent Sidereal Time)
특정 시점에 경도 0도(본초자오선)에서 측정한 실제의 항성시. GMST에 장동과 지구의 극운동을 반영한 값
지방 평균 항성시(LMST, Local Mean Sidereal Time)
특정 시점에 관측지에서 측정한 평균 항성시
지방 겉보기 항성시(LAST, Local Apparent Sidereal Time)
특정 시점에 관측지에서 측정한 실제의 항성시. GMST에 장동과 지구의 극운동을 반영한 값
이 가운데 관측에서 실제로 필요한 값은 지방 진항성시입니다. 지방 겁모기 항성시는 지방평균항성시와 각도로 약 10초 이내의 범위에서 일치하며 관측지에서 특정한 시각의 천체의 위치를 계산하는데 쓸 수 있습니다.
이 글에서는 IAU2006에서 결정한 방법에 따라 항성시를 계산하는 방법을 설명합니다. 현재 이 방법은 미국에서 발행하는 천문역서(The Astronomical Almanac)에서 쓰고 있습니다.
(1) 그리니치 평균 항성시(GMST)
IAU에서는 지구의 자전 속도를 일정하다고 가정하고 지구의 회전 속도를 정의했습니다. 이 값을 약어로 ERA(Rate of advance of Earth rotation angle)라고 부르며 이 값은 아래와 같습니다.
ERA = 1.00273781191135448 회전/일(UT1)
평균항성시는 ERA에서 정한 비율에 따라 회전한 만큼에 세차 운동에 의해 변화하는 양을 더한 값으로 산출할 수 있습니다.
GMST(Du, T) = θ(Du) + GMSTP(T)
θ(Du)는 ERA에서 정한 값에 따라 회전한 값이고 GMSTP(T) 는 세차운동에 의해 변하는 부분입니다. Du는 J2000.0 원기에서 계산 시점까지의 날짜 수, T는 J2000.0 원기에서 계산 시점까지의 시간 간격을 율리우스 세기로 나타낸 값입니다. Du와 T는 아래 식으로 계산할 수 있습니다. Du는 UT로, T는 TT로 계산해야합니다.
Du = JDUT1 - 2451545.0
T = (JDTT - 2451545.0) / 36525
θ(Du)와 GMSTP(T)는 다음 식으로 계산할 수 있습니다. 단위는 초(Arcsecond)입니다.
θ(Du) = 1296000"(0.7790572732640 + 0.00273781191135448Du + frac(Du))
GMSTP(T) = 0".014506 + 4612".156534T + 1".3915817T2 -0".00000044T3 - 0".000029956T4 - 3".68×10-8T5
frac(Du)는 Du의 소수점 부분입니다. 예을 들어 Du가 45.30432라면 frac(Du)는 0.30432가 됩니다. θ(Du)와 GMSTP(T) 식을 하나로 합치면 다음과 같이 됩니다.
GMST(Du, T) = θ(Du) + GMSTP(T)
= 1296000"(0.7790572732640 + 0.00273781191135448Du + frac(Du)) + 0".014506 + 4612".156534T + 1".3915817T2 -0".00000044T3 - 0".000029956T4 - 3".68×10-8T5
(2) 그리니치 겉보기 항성시 계산(GAST)
그리니치 겉보기 항성시는 그리니치 평균 항성시에 분점차(주로 장동운동으로 인한 것)를 더한 값입니다. 분점차(Equation of equinoxes)를 Ee라고 표시하면 그리니치 겉보기 항성시는 다음 식으로 표현할 수 있습니다.
GAST(Du, T) = GMST(Du, T) + Ee(T)
Ee(T)는 다음 식으로 계산할 수 있습니다.
Ee(T) = Δψ cos εA + Σk (C'k sin Ak + S'k cos Ak) - 0".00000087T sin Ω
이 식에서 Δψ는 장동운동으로 인한 황도방향의 변화량으로 이전에 설명한 장동 계산 글에 자세한 계산법이 설명되어 있습니다. εA는 계산 시점의 평균 황도 경사각입니다. 역시 이전의 글에서 계산 방법을 설명해 놓았습니다. Ω는 달의 평균 승교점 경도인데 다음 식을 이용해 계산할 수 있습니다.
Ω = 450160.398036 - 6962890.5431T + 7.4722T2 + 0.007702T3 - 0.00005939T4
Σk (C'k sin Ak + S'k cos Ak) 부분은 33개의 계산항으로 이루어진 식입니다. 이 부분의 계산법은 글의 끝 부분에 설명하겠습니다.
진항성시를 계산할 때 각별히 주의해야 할 부분이 있는데, 각각의 식에 쓰인 단위를 정확하게 맞추어 주어야 한다는 점입니다.
(3) 지방 항성시(LMST, LAST) 계산
그리니치 항성시에서 지방 항성시를 구하는 방법은 매우 간단합니다.
그리니치 항성시와 지방 항성시의 관계는 다음 식으로 간단히 나타낼 수 있습니다.
LMST = GMST + λ
LAST = GAST + λ
이 식에서 λ는 관측지의 경도입니다. ITRF나 WGS84 측지계로 나타낸 경도이며 동경은 (+), 서경은 (-)로 나타냅니다. 예를 들어 동경 128도는 +128°, 서경 35도는 -35°입니다.
지방 항성시를 아주 정밀하게 계산하고 싶다면 관측지의 경도에 극운동을 보정해 주어야 합니다. 극운동은 달과 여러 행성의 영향으로 나타나는데, 최대 0."3 정도의 크기로 나타납니다. 이 움직임은 미리 예측할 수는 없고 관측을 통해 결정해야합니다. 극운동의 관측치와 단기간(약 1년) 동안의 예측은 IERS 홈페이지에서 얻을 수 있습니다.
지구의 극운동 측정치 및 단기 예측값 얻기
IERS Bulletin A http://maia.usno.navy.mil/ser7/ser7.dat
IERS Bulletin B http://maia.usno.navy.mil/ser7/bulb.dat
위의 주소로 들어가면 극운동의 값 x와 y를 얻을 수 있습니다. 이 값을 바탕으로 관측지의 경도를 보정하려면 다음 식을 쓰면 됩니다. 식에 나오는 φITRS와 λITRS는 관측지의 위도와 경도(WGS84 또는 ITRS로 나타낸 위도)입니다. 이 식은 근사식으로 고위도 지역에서는 오차가 커질 수 있다는 점에 유의해야 합니다.
λ = λITRS + (x sin λITRS + y cos λITRS ) tan φITRS
(4) Σk (C'k sin Ak + S'k cos Ak) 부분 계산법
이 부분은 모두 34개의 계산항으로 이루어져 있습니다. 계산을 위해서는 달과 지구, 주요 행성의 위치 정보가 필요합니다. 이 위치 정보는 다음 식으로 계산할 수 있습니다(IAU2000/2006 장동식에 쓰는 계산식과 동일합니다).
먼저 태양과 달의 운동에 관한 식입니다. 단위는 모두 초(arcsecond, as)입니다.
l = 달의 평균 근점이각 = 485868.249036 + 1717915923.2178T + 31.8792T2 + 0.051635T3 - 0.00024470T4
l' = 해의 평균 근점이각 = 1287104.79305 + 129596581.0481T - 0.5532T2 + 0.000136T3 - 0.00001149T4
F = L - Ω = 335779.526232 + 1739527262.8478T - 12.7512T2 - 0.001037T3 + 0.00000417T4
D = 해와 달의 평균 이각 = 1072260.70369 + 1602961601.2090T - 6.3706T2 + 0.006593T3 - 0.00003169T4
Ω = 달의 승교점 경도 = 450160.398036 - 6962890.5431T + 7.4722T2 + 0.007702T3 - 0.00005939T4
(L = 달의 평균 황경)
행성의 운동에 관한 식입니다. 단위는 모두 초(arcsecond, as)입니다.
Lv = 금성의 평균 황경 = 655127.283060 + 210664136.433548T
Le = 지구의 평균 황경 = 361679.244588 + 129597742.283429T
행성과 달의 위치에 관한 식 외에도 지구의 일반세차량을 계산할 필요가 있습니다. 단위는 초(arcsecond, as)입니다.
Pa = 5028.8200T+ 1.112022T2
이 값을 모두 계산했으면 Σk (C'k sin Ak + S'k cos Ak) 부분을 계산할 수 있습니다. 아래 식에서 계수 C'k와 S'k의 단위는 마이크로초(microarcsecond)이므로 계산이 끝난 후 초(arcsecond) 단위로 바꾸려면 1000000으로 나누어 주어야 합니다.
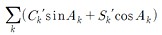
= 2640.96 sin(Ω) - 0.39 cos(Ω)
+ 63.52 sin(2Ω) - 0.02 cos(2Ω)
+ 11.75 sin(2F - 2D + 3Ω) + 0.01 cos(2F - 2D + 3Ω)
+ 11.21 sin(2F - 2D + Ω) + 0.01 cos(2F - 2D + Ω)
- 4.55 sin(2F - 2D + 2Ω)
+ 2.02 sin(2F + 3Ω)
+ 1.98 sin(2F + Ω)
- 1.72 sin(3Ω)
- 1.41 sin(l' + Ω) - 0.01 cos(l' + Ω)
- 1.26 sin(l' - Ω) - 0.01 cos(l' - Ω)
- 0.63 sin(l - Ω)
- 0.63 sin(l + 1Ω)
+ 0.46 sin(l' + 2F - 2D + 3Ω)
+ 0.45 sin(l' + 2F - 2D + Ω)
+ 0.36 sin(4F - 4D + 4Ω)
- 0.24 sin(F - D + Ω - 8Lv + 12Le) - 0.12 cos(F - D + Ω - 8Lv + 12Le)
+ 0.32 sin(2F)
+ 0.28 sin(2F + 2Ω)
+ 0.27 sin(l + 2F + 3Ω)
+ 0.26 sin(l + 2F + Ω)
- 0.21 sin(2F - 2D)
+ 0.19 sin(l' - 2F + 2D - 3Ω)
+ 0.18 sin(l' - 2F + 2D - Ω)
- 0.10 sin(8Lv - 13Le - Pa) + 0.05 cos(8Lv - 13Le - Pa)
+ 0.15 sin(2D)
- 0.14 sin(2l - 2F - Ω)
+ 0.14 sin(l - 2D + Ω)
- 0.14 sin(l' + 2F - 2D + 2Ω)
+ 0.14 sin(l - 2D - Ω)
+ 0.13 sin(4F - 2D + 4Ω)
- 0.11 sin(2F - 2D + 4Ω)
+ 0.11 sin(l - 2F - 3Ω)
+ 0.11 sin(l - 2F - Ω)
<참고문헌>
1. The Astronomical Almanac for the year 2010 (Washington, D.C.; 2008)
2. IERS Technical Note No. 32 chapter 5, http://www.iers.org/MainDisp.csl?pid=46-25776

 관측지 위치 구하기
관측지 위치 구하기


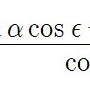


중요한 자료 잘 보고 있습니다.
수리천문에 나름대로 관심이 많아 자료를 여기저기 찾아보지만 국내에선 흔하지 않은 자료라 소중하게 생각하고 있습니다.
나름대로 외국서적을 거금을 들여 사서 독학하려니 힘듭니다...
천문학용어가 우리나라말로 통일된 안이 있는 지 궁금합니다.
님의 위 글중에,
그리니치 진항성시(GAST, GST, Greenwich Apparent Sidereal Time)
가 있는 데, 제가 이전에 자습하기로는
Apparent Sidereal Time 는 視(겉보기의 의미입니다)항성시로 알고 있었는 데,
이 것을 眞(true) 항성시로 번역하시는 이유가 있는 지 궁금해서 글 올립니다.
영어로도 true와 apparent는 분명히 구분되는 용어같은 데요...
감사합니다