평균 항성시와 평균 세계시(UT1)의 길이 비율은 세계시로 나타낸 하루의 길이를 항성시로 나타낸 하루의 길이로 나눈 비율입니다. 이 값은 지구가 얼마나 빠르게 자전하고 있는지를 나타내고 있으며, 이 값이 클수록 자전 속도가 느립니다. 기호로는 r'로 적습니다. 이 비율은 항성시 계산이나 ΔT의 추정에 이용됩니다.
항성시와 세계시의 관계를 식으로 적으면 아래와 같습니다. UT1은 세계시입니다.
(UT1의 길이) = r' × (항성시의 길이)
예를 들어 세계시로 표시한 하루(24시간)를 항성시로 나타내려면 24시간에 r'을 곱하면 됩니다. 2010년에는 r'의 값이 1.00273790935 이므로 세계시로 나타낸 하루를 항성시로 나타내면 1.00273790935 × 24(시간)이 됩니다.
2010년을 기준으로
1 평균 태양일(24시간) = 1.00273790935 평균 항성일(24시간 3분 56.55537초)
지구가 공전을 하고 있고 그 방향이 자전 방향과 같으므로, 평균 항성시와 평균 세계시(UT1)의 길이 비율은 항상 1보다 큰 값을 가집니다. 이 비율은 장기간에 걸쳐 대체로 일정한 편이지만 달과 해, 다른 행성의 조석력과 세차운동의 영향으로 인해 아주 느리게 변화합니다. 지금은 r' 값이 서서히 커지고 있습니다.
r'의 값은 아래 식으로 계산할 수 있습니다. T는 지구시로 계산해야 합니다. 아래에 소개한 세 개의 식 가운데 IAU2006 식이 가장 근래에 만들어진 식입니다. 새롭게 발행되는 천문력에서는 이 방식을 쓰고 있습니다.
T = (JDTT - 2451545.0) / 36525
IAU1980/1982
r' = 1.002737909350795 + 5.9006×10-11T - 5.9×10-15T2
IAU2000
r' = 1.00273790934498694 + 5.90107×10-11T - 5.92187×10-15T2 + 1.59032×10-15T3
IAU2006
r' = 1.00273790934496866 + 5.87954×10-11T - 2.78538×10-17T2 - 2.53133×10-15T3 - 3.88654×10-18T4
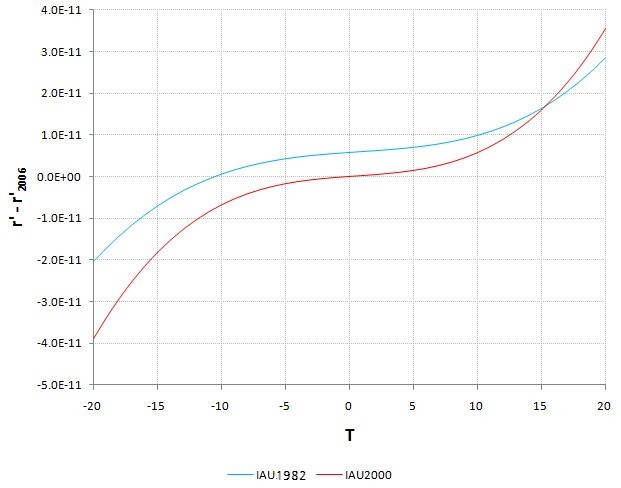
차이가 아주 작긴 하지만 계산식에 따라 r'의 값이 약간 다릅니다. IAU2006의 식을 기준으로 이 차이를 그래프로 그려보면 이렇습니다. 그래프에서 (r'-r'2006)의 값이 가장 큰 경우라도 오차는 2마이크로초 미만으로 실용상 세 식은 같은 결과를 준다고 해도 문제가 없는 정도입니다.
<참고 문헌>
1. Seidelmann, P. Kenneth, Explanatory supplement to the Astronomical Almanac (University Science Books, 1992)






정말 좋은 정보 잘보고 갑니다. 저도 열심히 공부해서 창환님과 같이 좋은 천문프로그램을 많이 만들도록 노력할께요. ^^