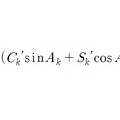천체의 좌표를 적도좌표에서 황도좌표 또는 황도좌표에서 적도좌표로 바꾸려면 아래 식을 쓰면 됩니다.
이 계산에 쓰이는 기호는 아래와 같습니다.
λ : 황경
β : 황위
α : 적경
δ : 적위
ε : 진황도경사각(True obliquity of the ecliptic)
(1) 적도좌표에서 황도좌표로 바꾸기
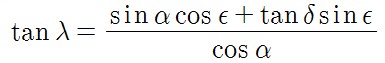
![]()
(2) 황도좌표에서 적도좌표로 바꾸기
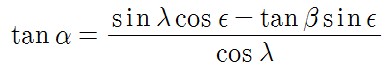
![]()
(3) 참고 사항
탄젠트 함수의 역함수를 이용해서 원래의 각도를 구할 때에는 원래의 각도가 어느 범위에 들어가는지 주의해야 합니다(적경과 황경을 계산할 떄 사용).
tan a = x
라고 할 때, 각 a는
tan-1 x = a1
로 구할 수 있습니다. 그런데 역탄젠트 함수로 계산한 a1는 -90° ≤ a1 ≤ 90° 의 범위를 가지므로 원래의 a와 역탄젠트 함수로 계산한 a1은 서로 다른 값을 가질 수도 있습니다. 따라서 원래의 각 a가 어떤 사분면에 위치하는지 검사해야 합니다.
직교좌표로 나타낸 점 P의 좌표를 x, y로 나타내면 탄젠트 함수는 다음과 같은 형태로 나타낼 수 있습니다. 각 a는 점 P와 x축 사이의 각도입니다.
tan a = y / x
각 a가 어느 사분면에 위치하고 있는지는 x와 y의 부호로 알 수 있습니다.
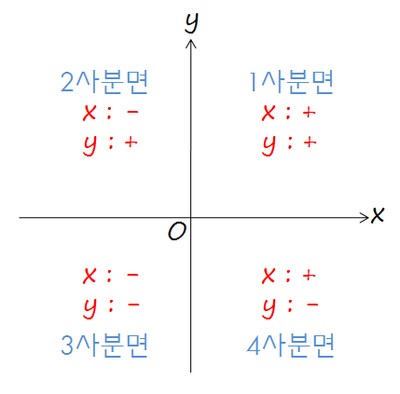
이 원리를 이용하면, x와 y 값의 부호를 알 수 있는 경우 역탄젠트 함수를 이용하더라도 원래의 각 a를 정확하게 알 수 있습니다.
이 좌표 변환(적도좌표↔황도좌표)에서는 분모와 분자에 있는 값을 그대로 x, y 값으로 대입시켜 계산할 수 있습니다. 예를 들어
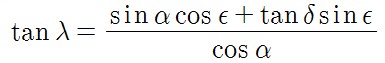
식에서
x = cos α
y = sin α cos ε + tan δ sin ε
로 대입을 하면, 각 λ가 자리하고 있는 사분면을 구할 수 있습니다.
C언어 같은 일부 컴퓨터 프로그램 언어에서는 역탄젠트 함수에서 사분면을 직접 판단할 수 있도록 atan2(y,x) 함수를 제공하고 있습니다. 이런 함수를 제공하는 프로그램 언어를 쓰고 있다면 아래와 같은 형태로 프로그램을 작성하면 됩니다.
lambda = atan2(sin(alpha) * cos(epsilon) + tan(delta) * sin(epsilon), cos(alpha))
*파란색 부분이 Y, 빨간색 부분이 X.
<참고 문헌>
1. J. Meeus, Astronomical Algorithms (Willmann-Bell, 1998)